Si, si, el título del artículo se podría decir que es un poco Click Bait, sin embargo si que os vamos a contar como cifrar datos utilizando varios algoritmos entre los que se encuentra AES-256. AES o Estándar de Encriptado Avanzado (de sus siglas en inglés Advanced Encryption Standar) es el algoritmo seleccionado oficialmente por el gobierno federal de los Estados Unidos. La versión con clave de 256 bits, conocida como AES-256 (eso no lo visteis venir eh?) se considera actualmente (en 2024, para los que leáis esto en el futuro), como el algoritmo de cifrado simétrico más seguro.

El código de este artículo va a ser muy fácil de seguir si habéis leído el artículo anterior. Sino, os recomiendo que lo hagáis, ya que la forma de cifrar y descrifrar datos es muy parecida a la forma de generar hashes y no vamos a volver a repetir aquí los conceptos básicos. Así que, sino has leído ese articulo, este es un buen momento pare hacer y así, entender mejor lo que sigue.

Códigos de Bloque y Códigos de Secuencia

Según la forma en la que el algoritmo de cifrado consume los datos de entrada, podemos clasificarlos en dos tipos: Bloque y Secuencia.

Los primeros consumen datos de entra en bloques de un tamaño definido, mientras que los segundos los consumen bit a bit y suelen ser más comunes en implementaciones HW. En este artículo vamos a hablar de cifrados de bloque, en concreto de AES como ya os adelantamos. Pero primero tenemos que introducir un par de conceptos para poder entender lo que sigue.

Un cifrado de bloque define un determinado tamaño de bloque con el que va a trabajar. Y eso tiene dos consecuencias fundamentales. La primera es que, normalmente la clave necesaria por el algoritmo suele ser del mismo tamaño que el bloque (más sobre esto enseguida) y la segunda es… que pasa cuando no tenemos suficientes datos para llenar el último bloque de nuestro mensaje cifrado?

Imaginemos que nuestro tamaño de bloque es de 128 bits o si lo preferís 16 bytes. Este es de hecho el caso para el algoritmo AES, independientemente del tamaño de la clave que utilicemos.

Ahora imaginad que tenemos que cifrar un mensaje de 17 bytes. El algoritmo toma los primeros 16 bytes y hace sus cosas para generar un nuevo bloque de 16 bytes cifrado, pero que hacemos con el último byte que nos queda por cifrar?. La respuesta es rellenar o hacer Padding como dicen en inglés, de forma que tengamos un nuevo bloque que cifrar con nuestro algoritmo.

Sin embargo, no podemos coger simplemente el primer byte del bloque cifrado. Tenemos que almacenar todo el bloque y disponer de un método para saber que solo un byte del último bloque forma parte del mensaje original. Así que, en general, cuando ciframos un mensaje con un algoritmo de bloque, el mensaje resultado siempre tendrá un tamaño mayor o como mucho igual al mensaje original.

Padding

Hay distintas estrategias para rellenar el bloque final, pero solo os vamos a comentar dos de ellas. Para más información hay un excelente artículo en la wikipedia sobre el tema.

La forma más sencilla de rellenar el último bloque es usar ceros. Si estamos cifrando cadenas de texto, el cero ya es un indicador de fin de cadena, pero en el caso general, necesitaríamos algún tipo de cabecera que nos informara del tamaño original. Super sencillo.

El otro tipo de relleno del que vamos a hablar es el utilizado por OpenSSL y por eso nos interesa. Se conoce como PKCS#7 y está descrito en el RFC5652. Este método consiste en rellenar los espacios pendientes con el número de espacios pendientes en el último bloque. Imaginemos que nuestro tamaño de bloque es de 8 bytes, en este caso tendríamos las siguientes posibilidades:

| XX XX XX XX XX XX XX XX | XX 07 07 07 07 07 07 07 |
| XX XX XX XX XX XX XX XX | XX XX 06 06 06 06 06 06 |   
| XX XX XX XX XX XX XX XX | XX XX XX 05 05 05 05 05 |       
| XX XX XX XX XX XX XX XX | XX XX XX XX 04 04 04 04 |           
| XX XX XX XX XX XX XX XX | XX XX XX XX XX 03 03 03 |               
| XX XX XX XX XX XX XX XX | XX XX XX XX XX XX 02 02 |                   
| XX XX XX XX XX XX XX XX | XX XX XX XX XX XX XX 01 |                       

Esos son todos los posibles patrones para el bloque final de un código bloque con tamaño 8 bytes. Si os fijáis, el último bloque es problemático. Que pasaría si en lugar de tener un byte que rellenar, tuviéramos un bloque entero cuyo ultimo byte es 01?… No podríamos diferenciarlo de otro bloque al que le faltase el último byte. Lo que PKCS#7 hace en este caso es añadir un bloque extra cuyo contenido es el tamaño del bloque. Así, en el caso de que el tamaño del mensaje es multiplo del tamaño de bloque (es decir, el último bloque está relleno), el mensaje que generaría PKCS#7 sería:

| XX XX XX XX XX XX XX XX | 08 08 08 08 08 08 08 08 |

Como veremos en breve, OpenSSL genera siempre un bloque de datos extra puesto que utiliza este tipo de rellenado.

Encriptando datos

Ahora que estos pequeños detalles de implementación han sido aclarados, veremos que el proceso de encriptar y desencriptar datos es muy sencillo. Comenzaremos viendo el código para encriptar un mensaje con más detalle ya que el proceso de descriptado es prácticamente idéntico.

Vamos a utilizar un sencillo programa que encripta y desencripta un mensaje que recibe de la entrada estándar. Como veréis el API que ofrece OpenSSL es muy fácil de usar y podréis modificarlo muy fácilmente para escribir vuestras propias utilidades.

Dividiremos el código en dos partes. La primera cifra el mensaje, y la podéis ver a continuación. La segunda lo descifra y la tenéis que añadir tras esta parte, ya que usa las mismas variables y claves que la primera parte.

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <openssl/evp.h>

int main (int argc, char *argv[]) {
  unsigned char key[] = {
    0xC7, 0x75, 0xE7, 0xB7, 0x57, 0xED, 0xE6, 0x30,
    0xCD, 0x0A, 0xA1, 0x11, 0x3B, 0xD1, 0x02, 0x66,
    0x1A, 0xB3, 0x88, 0x29, 0xCA, 0x52, 0xA6, 0x42,
    0x2A, 0xB7, 0x82, 0x86, 0x2F, 0x26, 0x86, 0x46
  };
  unsigned char iv[] = {
    0x15, 0x25, 0x35, 0x45, 0x55, 0x65, 0x75, 0x85,
    0x16, 0x26, 0x36, 0x46, 0x56, 0x66, 0x76, 0x86
  };
  char               txt[1024];
  unsigned char      txt_enc[1024];
  long unsigned long txt_len = 0;
  long unsigned long txt_enc_len = 0;
  int                len, r;

  const EVP_CIPHER *c = EVP_get_cipherbyname (argv[1]);
  size_t bsize = EVP_CIPHER_get_block_size(c);

  // Initializamos los buffers
  memset (txt, 0, 1024); 
  memset (txt_enc, 0, 1024);
  
  // Leemos un mensaje de la entrada estándard
  printf ("%s", "Mensaje ? \n");
  fgets (txt, 1024, stdin);
  
  txt_len = strlen(txt);
  txt_enc_len = 0;
  
  // Creamos un contexto de cifrado y lo inicializamos
  EVP_CIPHER_CTX *ctx;
  ctx = EVP_CIPHER_CTX_new();
  EVP_EncryptInit (ctx, c, key, iv);
  // Mientras tengamos bloques que cifrar.... Ciframos
  while (txt_len > bsize) {
    r = EVP_EncryptUpdate (ctx, txt_enc + txt_enc_len, &len, 
                                txt     + txt_enc_len, txt_len);
    txt_enc_len += len;
    txt_len -= len;
  }
  len = 0;
  // Procesa cualquier dato que quede pendiente
  EVP_EncryptFinal (ctx, txt_enc + txt_enc_len, &len);
  txt_enc_len += len;
  // Liberamos el contexto
  EVP_CIPHER_CTX_free (ctx);
  printf ("Total mensaje cifrado : %d\n", txt_enc_len);
  BIO_dump_fp (stdout, txt_enc, txt_enc_len);
  
  // Descifrado
  // (...)

Seleccionando el cifrado

Lo primero que hace el programa es seleccionar el tipo de cifrado que vamos a utilizar, el cual pasaremos como primer parámetro al programa. Una vez seleccionado determina el tamaño de bloque del algoritmo en cuestión. Y ya sabemos por que eso es importante.

  const EVP_CIPHER *c = EVP_get_cipherbyname (argv[1]);
  size_t bsize = EVP_CIPHER_get_block_size(c);

Para obtener una lista de los posibles algoritmos, podemos utilizar la utilidad openssl. En nuestro sistema obtenemos la siguiente salida

$ openssl
(...)
Cipher commands (see the `enc' command for more details)
aes-128-cbc       aes-128-ecb       aes-192-cbc       aes-192-ecb
aes-256-cbc       aes-256-ecb       aria-128-cbc      aria-128-cfb
aria-128-cfb1     aria-128-cfb8     aria-128-ctr      aria-128-ecb
aria-128-ofb      aria-192-cbc      aria-192-cfb      aria-192-cfb1
aria-192-cfb8     aria-192-ctr      aria-192-ecb      aria-192-ofb
aria-256-cbc      aria-256-cfb      aria-256-cfb1     aria-256-cfb8
aria-256-ctr      aria-256-ecb      aria-256-ofb      base64
bf                bf-cbc            bf-cfb            bf-ecb
bf-ofb            camellia-128-cbc  camellia-128-ecb  camellia-192-cbc
camellia-192-ecb  camellia-256-cbc  camellia-256-ecb  cast
cast-cbc          cast5-cbc         cast5-cfb         cast5-ecb
cast5-ofb         des               des-cbc           des-cfb
des-ecb           des-ede           des-ede-cbc       des-ede-cfb
des-ede-ofb       des-ede3          des-ede3-cbc      des-ede3-cfb
des-ede3-ofb      des-ofb           des3              desx
rc2               rc2-40-cbc        rc2-64-cbc        rc2-cbc
rc2-cfb           rc2-ecb           rc2-ofb           rc4
rc4-40            seed              seed-cbc          seed-cfb
seed-ecb          seed-ofb          sm4-cbc           sm4-cfb
sm4-ctr           sm4-ecb           sm4-ofb

Nuestro programa podrá utilizar cualquiera de estos algoritmos para cifrar nuestros datos. Como podéis ver, para cada algoritmo hay varias opciones. Algunas indican el tamaÑo de clave, como sucede con aes, aria o camellia, mientras que otras definen modos de operación como los terminados en -cbc o -ecb por ejemplo. Hablaremos de esto un poco más tarde.

Cifrando datos

El proceso de cifrado con el API EVP_ de OpenSSL es igual al proceso de generación de hashes, pero con códigos de cifrado en lugar de con funciones hash. Así que los pasos son los mismos:

• Genera un objeto contexto para mantener el estado de nuestro cifrado
• Inicializa el cifrado con los valores necesarios
• Pasa la información a cifrar al contexto y almacena el resultado
• Procesa lo que este pendiente y terminar

Si comparamos este código con el que usamos para generar hashes podemos ver dos diferencias principales (dejando a un lado el nombre de las funciones)

  EVP_CIPHER_CTX *ctx = EVP_CIPHER_CTX_new();
  EVP_EncryptInit (ctx, c, key, iv);

  while (txt_len > bsize) {
    r = EVP_EncryptUpdate (ctx, txt_enc + txt_enc_len, &len, 
                                txt + txt_enc_len, txt_len);
    txt_enc_len += len;
    txt_len -= len;
  }
  EVP_EncryptFinal (ctx, txt_enc + txt_enc_len, &len);
  text_enc_len += len;
  EVP_CIPHER_CTX_free (ctx);
  
  BIO_dump_fp (stdout, txt_enc, txt_enc_len);

La primera es que en la función de inicialización es en la que pasamos la clave y el vector inicial. Olvidaros por ahora del vector de inicialización IV, volveremos sobre esto un poco más tarde.

La segunda es que cuando llamamos a EVP_EncryptUpdate tenemos que incrementar ambos punteros el de los datos originales y el del resultado. Recordad que con el hash, los resultado siempre se almacenaban en el mismo sitio, pero aquí tenemos que cifrar los datos originales y cada bloque que cifremos tenemos que almacenarlo en su correspondiente bloque de memoria.

La función EVP_EncryptUpdate permite utilizar el mismo buffer como entrada y salida siempre que almacenemos los datos en el mismo sitio de donde los sacamos. En este caso hemos decidido utilizar dos buffers separados por claridad. Pero que lo sepáis…

La otra es que, como comentamos cuando hablamos del Padding, debemos procesar los datos hasta que nos queden menos bytes que los que conforman un bloque (condición en el while), y finalmente llamar a EVP_EncryptFinal para procesar ese último bloque, ya sea el que hemos rellenado o hemos añadido según el algoritmo PKCS#7.

A parte de eso, como podéis ver, la forma de cifrar datos es muy,muy sencilla. Una vez que los datos están cifrados, en este programa de ejemplo, nosotros los volcamos en la consola, para echarles un ojo. Podríamos escribir nuestra propia función, pero en este caso utilizamos la función BIO_dump_fp que propociona OpenSSL.

Desencriptando datos

Lo prometido es deuda, y aquí tenéis la segunda parte del programa que desencripta los datos que acabamos de encriptar. Simplemente añadid este código a continuación del primero para tener el programa completo.

  // Destruir el buffer de texto plano
  memset (txt, 0, 1024); 
  txt_len = 0;

  // Creammos e inicializamos un nuevo contexto de cifrado
  ctx = EVP_CIPHER_CTX_new();
  EVP_DecryptInit (ctx, c, key, iv);

  // Mientras tengamos datos pendientes, desencriptamos
  while (txt_enc_len > bsize) {
    EVP_DecryptUpdate (ctx, txt+txt_len, &len, txt_enc+txt_len, txt_enc_len);
    txt_len += len;
    txt_enc_len -= len;
  }
  len = 0;
      BIO_dump_fp (stdout, txt, txt_len);
  if ((r = EVP_DecryptFinal (ctx, txt + txt_len, &len)) == 0) 
    fprintf (stderr, "Datos de entrada corruptos\n");
  txt_len += len;
  BIO_dump_fp (stdout, txt, txt_len);
  EVP_CIPHER_CTX_free (ctx);
  }

Como podéis ver el código es casi idéntico. Procesamos todos los bloques excepto el último. Puesto que no hemos desactivado el padding, el último bloque es siempre un bloque de padding y debe ser procesado con EVP_Decrypt_Final. Esta función comprobará cuantos bytes de padding fueron usados y nos devolverá en len el número de bytes final que debemos añadir a nuestro buffer.

Al final del programa volcamos el buffer con el tamaño real, tras la correción con el valor devuelto por EVP_DecryptFinal y con el tamaño de bloque, para que podáis ver el padding.

Probando nuestro ejemplo

Es hora de compilar y probar nuestro ejemplo. Para compilar este programa tenemos que utilizar la librería libcrypto tal que así:

$ gcc -g -o acrypt acrypt.c -lcrypto

Y ahora ya podemos ejecutarlo con distintos algoritmos. Estos son algunos ejemplos. Primero veamos que sucede cuando la entrada es un múltiplo de bloque.

# (perl -e 'print "A"x64;'| ./k aes-256-ecb)
Mensaje ?
Total mensaje cifrado : 80
0000 - 2e bf 50 07 e2 c0 d6 60-d8 f3 dc 96 71 c1 e8 72   ..P....`....q..r
0010 - 2e bf 50 07 e2 c0 d6 60-d8 f3 dc 96 71 c1 e8 72   ..P....`....q..r
0020 - 2e bf 50 07 e2 c0 d6 60-d8 f3 dc 96 71 c1 e8 72   ..P....`....q..r
0030 - 2e bf 50 07 e2 c0 d6 60-d8 f3 dc 96 71 c1 e8 72   ..P....`....q..r
0040 - 82 34 3f 32 92 bb 77 28-82 70 35 7e d8 40 e8 5f   .4?2..w(.p5~.@._
------------------------------
0000 - 41 41 41 41 41 41 41 41-41 41 41 41 41 41 41 41   AAAAAAAAAAAAAAAA
0010 - 41 41 41 41 41 41 41 41-41 41 41 41 41 41 41 41   AAAAAAAAAAAAAAAA
0020 - 41 41 41 41 41 41 41 41-41 41 41 41 41 41 41 41   AAAAAAAAAAAAAAAA
0030 - 41 41 41 41 41 41 41 41-41 41 41 41 41 41 41 41   AAAAAAAAAAAAAAAA

Como podéis ver, al cifrar 64 bytes que es un múltiplo del tamaño de bloque de AES-256, durante el cifrado añadimos un nuevo bloque con el valor 0x10 que representa el padding PKCS. También podemos ver como, tras utilizar el valor devuelto por EVP_DecryptFinal obtenemos el tamaño correcto del mensaje original.

Veamos que pasa si nos pasamos por dos bytes.

# (perl -e 'print "A"x66;'| ./k aes-256-ecb)
Mensaje ?
Total mensaje cifrado : 80
0000 - 2e bf 50 07 e2 c0 d6 60-d8 f3 dc 96 71 c1 e8 72   ..P....`....q..r
0010 - 2e bf 50 07 e2 c0 d6 60-d8 f3 dc 96 71 c1 e8 72   ..P....`....q..r
0020 - 2e bf 50 07 e2 c0 d6 60-d8 f3 dc 96 71 c1 e8 72   ..P....`....q..r
0030 - 2e bf 50 07 e2 c0 d6 60-d8 f3 dc 96 71 c1 e8 72   ..P....`....q..r
0040 - bb f1 ef 09 1b 99 d0 4c-d1 30 bd b4 e9 5a 15 70   .......L.0...Z.p
------------------------------
0000 - 41 41 41 41 41 41 41 41-41 41 41 41 41 41 41 41   AAAAAAAAAAAAAAAA
0010 - 41 41 41 41 41 41 41 41-41 41 41 41 41 41 41 41   AAAAAAAAAAAAAAAA
0020 - 41 41 41 41 41 41 41 41-41 41 41 41 41 41 41 41   AAAAAAAAAAAAAAAA
0030 - 41 41 41 41 41 41 41 41-41 41 41 41 41 41 41 41   AAAAAAAAAAAAAAAA
0040 - 41 41                                             AA

Mismo resultado, solo que ahora podemos ver el algoritmo de padding en vivo. Al usar solo dos bytes del último bloque, debemos añadir 14 bytes para completar el bloque que, en hexadecimal es 0x0e.

Bueno, parece que funciona bastante bien. Podéis obtener una lista de los algoritmos disponibles en vuestro sistema utilizando el comando:

openssl list -cipher-algorithms

Porque no me puedo cifrar con rc4?

Has probado a pasar como parámetro a nuestro programa rc4 o bf y no ha sucedido nada?. No te preocupes, ahora mismo lo solucionamos. Lo primero que debemos hacer es modificar nuestro programa ligeramente para que nos muestre mensajes de error, para ello debemos añadir el fichero de cabecera <openssl/err.h>. Ahora podemos realizar la siguiente modificación:

#include <openssl/provider.h>
(...)
main (...)

  while (txt_len >= bsize) {
    r = EVP_EncryptUpdate (ctx, txt_enc + txt_enc_len, &len, 
                        txt     + txt_enc_len, txt_len);
    if (!r) {ERR_print_errors_fp (stderr);exit (1);}
    txt_enc_len += len;
    txt_len -= len;
    }
(...)

La función EVP_EncryptUpdate retorna 0 si se produce un error. Si ahora recompilamos y ejecutamos esta nueva versión de nuestro programa obtendríamos:

$ (perl -e 'print "A"x65;'| ./k bf)
BLock Size : 8 (0x7f7530432b80)
Mensaje ?
40E7DE2F757F0000:error:0308010C:digital envelope routines:inner_evp_generic_fetch
:unsupported:../crypto/evp/evp_fetch.c:373:Global default library context, 
Algorithm (BF-CBC : 11), Properties ()
40E7DE2F757F0000:error:03000083:digital envelope routines:EVP_EncryptUpdate:
no cipher set:../crypto/evp/evp_enc.c:665:

Si bien el mensaje parece que está cifrado con el propio algoritmo bf (que es como OpenSSL conoce al algoritmo BlowFish), lo que realmente nos está diciendo es que no puede encontrar ese algoritmo para utilizarlo.

Las versiones más modernas de OpenSSL, están configuradas por defecto para no utilizar algoritmos que se no se consideran seguros. OpenSSL utiliza lo que ellos llaman proveedores (Providers en inglés). Existen varios tipos pero los que nos interesan son los proveedores por defecto y los llamados legacy que incluyen algoritmos digamos… viejos u obsoletos. Podemos activar eso algoritmos legacy modificando el fichero de configuración de OpenSSL, o añadiendo unas pocas líneas de código a nuestro programa.

En cualquier caso, todos los detalles los podéis encontrar en el fichero README-PROVIDERS.md del github official de OpenSSL.

Tamaños de bloque y Claves

En los primeros algoritmos criptográficos, como DES (Data Encription Standard), el tamaño de la clave coincidía con el tamaño del bloque. En los algoritmos actuales ese ya no es el caso. Por ejemplo, AES-256 utiliza una clave de 256 bits, pero su tamaño de bloque es de 128 bits. AES-128 utiliza una clave de 128 bits, aunque su tamaño de bloque es también 128 bits.

Lo que estos nuevos tipos de cifrado utilizan es un algoritmo de transformación de la clave original. Estos algoritmos se suelen conocer como Key Schedule, algo así como planificación de clave. A veces se utilizan para crear claves más pequeñas a partir de claves mayores, o si lo preferís muchas claves de un determinado tamaño (como AES), otras para generar una clave más grande a partir de una más corta (como en RC4).

Lo que es importante tener claro es que si bien el tamaño del bloque y el tamaño de clave no tienen porque coincidir, de alguna forma, internamente es necesario utilizar una clave del tamaño del bloque usado por el algoritmo y cuando ese no es el caso, existen algoritmos para conseguir claves del tamaño adecuado, a partir de la clave original. Para entender lo que significa este último párrafo y saber para que es esa variable iv de la que no hemos dicho nada a propósito, tenemos que introducir los modos de cifrado.

Modos de cifrado

Recordáis el Vector de Inicializacion (IV en inglés) del que hablamos al principio?. Bueno, es hora de volver sobre este tema. Pero primero quiero mostraros algo:

# (perl -e 'print "A"x64;'| ./k aes-256-ecb)
BLock Size : 16 (0x7f6eaa38b740)
Mensaje ?
Total mensaje cifrado : 80
0000 - 9e 9d 05 b2 b8 8e 96 1c-1d e0 0c 90 27 9e a3 42   ............'..B
0010 - 9e 9d 05 b2 b8 8e 96 1c-1d e0 0c 90 27 9e a3 42   ............'..B
0020 - 9e 9d 05 b2 b8 8e 96 1c-1d e0 0c 90 27 9e a3 42   ............'..B
0030 - 9e 9d 05 b2 b8 8e 96 1c-1d e0 0c 90 27 9e a3 42   ............'..B
0040 - 31 c7 81 8d 54 9d c2 6c-c1 8b 04 71 38 42 17 8d   1...T..l...q8B..
(...)

Como podéis ver, si utilizamos el modo ECB (Electronic Code Book o Libro de códigos electrónico), vemos como los primeros 16 bytes (el tamaño de bloque de AES) se repiten en bloques sucesivos, excepto para el último bloque, el cual, si recordáis, es un bloque de relleno que contiene el valor 0x10 repetido. A primera vista esto no parece un grave problema, pero, puesto que, bloques idénticos en el fichero original se codificaran de la misma forma, ciertos patrones se podrán identificar incluso si el fichero está cifrado. Al final del artículo veremos un ejemplo práctico.

Para evitar este problema se introdujeron formas de manejar los datos para que una misma secuencia de bytes no produzca siempre el mismo resultado. Básicamente, estos modos de cifrado simplemente toman algún dato del bloque anteriormente cifrado y lo usan para modificar los datos de entrada en el siguiente bloque. Existen 4 modos de cifrado clásicos:

• ECB Electronic Code Book. Este es el modo básico en el que los datos de entrada se dividen en bloques y cada uno de ellos se cifra tal cual utilizando la clave proporcionada por el usuario.
• CBC Cipher Block Chaining. En este modo, cada uno de los bloques de datos a cifrar se modifican aplicando una operación xor con el resultado del cifrado del bloque anterior.
• CFB Cipher FeedBack. En este modo, cada bloque de datos cifrados se calcula aplicando una operación xor entre el bloque sin cifrar y el resultado del cifrado del bloque anterior.
• OFB Ouput Feedback. Este modo funciona igual que el anterior, pero en lugar de pasar como entrada al siguiente bloque el resultado del xor con el texto plano, envía la salida del bloque actual.

En la actualidad se han definido algunos modos más, sin embargo, conceptualmente, todos funcionan igual, así que, sin pérdida de generalidad, como dicen los matemáticos, vamos a hablar solo de el modo CBC.

El infame IV

Como acabamos de decir, vamos a centrarnos, a modo de ejemplo, en el modo CBC. Veamos el diagrama de bloques de este modo:

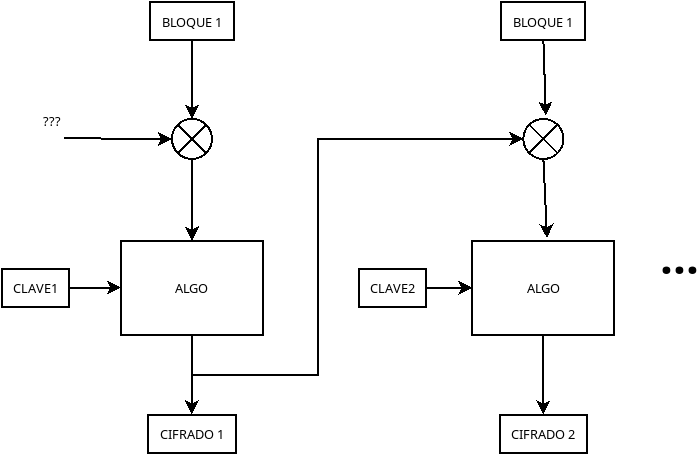
Para el caso de AES-256, en el diagrama anterior, los bloques de entrada (BLOQUE1 y BLOQUE2) contienen los datos a encriptar en bloques de 128 bits. Recordad el tamaño de bloque para AES es de 128 bits independientemente de la clave. Ahora ya sabéis lo que esto significa… cada bloque de 16 bytes es lo que se pasa por la caja que hemos llamado ALGO en el diagrama.

Cada uno de los bloques ALGO implementan el algoritmo de cifrado seleccionado, el cual necesita la clave del usuario para funcionar. Para AES, esa clave debe ser también de 128 bits y como podéis ver es un parámetro de entrada para cada uno de los bloques ALGO. Cada una de esas CLAVEs son calculadas a partir de la clave original utilizando un algoritmo de varios pasos. Dependiendo del tamaño de la clave (128, 192 o 256), el algoritmo aplica un número determinado de iteraciones para generar la clave de 128bits que necesitamos para cada bloque.

La salida del ALGO es el resultado del cifrado del bloque inicial. Es en este momento en el que el modelo de cifrado CBC entra en juego. Ese mismo resultado del primer cifrado se propaga al siguiente bloque en el que realizamos un XOR entre este resultado y el siguiente bloque a cifrar. De esta forma, conseguimos que aunque BLOQUE1 y BLOQUE2 sean exactamente iguales, el resultado del cifrado de estos dos bloques será totalmente diferente, puesto que estamos modificando la entrada al algoritmo. La operación XOR es muy guay por que es muy fácil de invertir.

Bien, y aquí es donde entra en juego el infame IV. Si os fijáis, utilizamos la salida de cada etapa de cifrado para modificar los datos de entrada a la siguiente. Esto funciona genial, para todas las etapas menos para la primera. Y ahí lo tenéis, ese es el IV el valor que utilizamos en la primera etapa (por eso lo de inicialización) para modificar los datos del primer bloque a cifrar.

Cuando trabajamos en modo ECB cada uno de los bloques del diagrama anterior es independiente (no hay datos que pasan de una etapa a otra) y por lo tanto no necesitamos un vector de inicialización. Como podéis observar, nuestro programa siempre pasa un valor de IV al CIPHER sin embargo, para los modos ECB, ese valor simplemente se ignora.

En general, el valor de IV no tiene por que ser secreto pero si aleatorio o, dependiendo del tipo de algoritmo con el que lo usemos, solo es necesario que sea impredecible o único. Este valor normalmente se almacena junto con los datos cifrados ya que es necesario para poder decodificar el mensaje si bien, conocer su valor no ofrece ninguna información útil para descifrar el mensaje.

IV en AES-256

Con todo esto nuevo que sabemos, vamos a echar un ojo, una vez más, a la salida de nuestro programa cuando utilizamos el modo ECB con un patrón claramente definido:

$ (perl -e 'print "A"x64;'| ./k aes-256-ecb)
BLock Size : 16 (0x7f6eaa38b740)
Mensaje ?
Total mensaje cifrado : 80
0000 - 9e 9d 05 b2 b8 8e 96 1c-1d e0 0c 90 27 9e a3 42   ............'..B
0010 - 9e 9d 05 b2 b8 8e 96 1c-1d e0 0c 90 27 9e a3 42   ............'..B
0020 - 9e 9d 05 b2 b8 8e 96 1c-1d e0 0c 90 27 9e a3 42   ............'..B
0030 - 9e 9d 05 b2 b8 8e 96 1c-1d e0 0c 90 27 9e a3 42   ............'..B
0040 - 31 c7 81 8d 54 9d c2 6c-c1 8b 04 71 38 42 17 8d   1...T..l...q8B..
(...)

Los primeros cuatro bloques idénticos se deben a que la implementación de ECB de OpenSSL utiliza bloques de 16 bytes como ya hemos visto. Como cada etapa de cifrado es independiente, obtenemos 4 bloques idénticos. El último bloque es el de relleno y por lo tanto es diferente a los anteriores.

Si utilizáramos el modo CBC, el resultado es bastante diferente:

$ (perl -e 'print "A"x64;'| ./k aes-256-cbc)
BLock Size : 16 (0x7f5382f33940)
Mensaje ?
Total mensaje cifrado : 80
0000 - 51 c8 0e f0 60 34 5b 67-a1 60 45 4a 9d 88 2d ac   Q...`4[g.`EJ..-.
0010 - c0 a1 c0 6b db 0e 34 11-4e 06 04 15 f2 f3 0c 36   ...k..4.N......6
0020 - b1 ea a6 8f f1 10 1c 97-d7 ea 25 79 cc 09 01 88   ..........%y....
0030 - 50 51 b8 9a 76 31 3c 23-48 2c 3a 1f f4 1a c7 29   PQ..v1<#H,:....)
0040 - ea c5 9b 05 ee 46 4f 69-da cb 7a 37 38 6f 7e 72   .....FOi..z78o~r

Como podemos ver, ahora cada bloque es diferente y no se puede deducir nada sobre la secuencia de datos original. En este sencillo ejemplo, esto no parece un problema muy grave, pero bajo ciertas circunstancias y dependiendo de nuestro caso de uso puede ser un problema. Veamos un ejemplo.

Seleccionad una imagen que contenga un dibujo, es decir, una imagen que tenga grandes áreas con un mismo color. Yo he elegido a nuestro querido Tux.

Imagen de la mascota de Linux. Tux

Ahora convertiremos nuestra imagen al formato PGM. Este formato no tiene nada de especial, simplemente, como veremos en un segundo, hará más fácil manipular la imagen de la forma que necesitamos.

$ convert tux.jpg tux.pgm

Necesitaréis el paquete imagemagick para poder disponer de la utilidad convert

Lo interesante de el formato PGM es que la cabecera son solo 3 líneas de texto. En nuestro caso está (con la imagen de Tux de la wikipedia) es la cabecera.

P5
1727 2047
255

Ahora debemos eliminar estas 3 líneas. Puedes abrir el fichero en tu editor de textos favorito y borrarlas o:

$ sed -i '1,3d' tux.pgm

Ahora encriptamos el fichero con la utilidad openssl o quizás utilizando tu propio program ;).

openssl enc -aes-256-cbc -p -in tux.pgm -out tux-cbc.enc
openssl enc -aes-256-ecb -p -in tux.pgm -out tux-ecb.enc

Ahora solo tenemos que poner la cabecera otra vez a los ficheros:

$ cat << EOM > file1.pgm
> P5
> 1727 2047
> 255
> EOM
$ cp file1.pgm file2.pgm
$ cat tux-cbc.enc >> file1.pgm
$ cat tux-ecb.enc >> file2.pgm

Ahora abre los ficheros con tu visor de imágenes preferido y verás cual es el problema con el modo ECB. Os reproducimos las dos imágenes aquí para los más holgazanes.

Conclusiones

En este pequeño artículo hemos visto como utilizar OpenSSL para encriptar y desencriptar datos utilizando cualquiera de los algoritmos que nos proporciona. Hemos prestado algo más de atención a AES ya que es el algoritmo simétrico más seguro hasta la fecha y hemos visto los principales modos de cifrado (hay algunos más) con los que utilizar algoritmos de cifrado por bloque como AES, lo cual nos ha permitido entender la función del vector de inicialización (normalmente referido como IV) que se ve de vez en cuando por ahí.